Mô Hình Sản Sinh Dữ Liệu (Generative Model)

Trong phần đầu tiên của blog, chúng ta đã thảo luận về ứng dụng của định lý tích phân Fourier (Fourier integral theorem) cho vấn đề ước lượng hàm mật độ trong khoa học dữ liệu và học máy (Xem thêm tại đây). Trong phần thứ hai của blog này, chúng ta sẽ thảo luận về một ứng dụng quan trọng khác của định lý tích phân Fourier trong việc phát triển mô hình sản sinh dữ liệu (generative model).

Một câu hỏi tự nhiên ở đây là vì sao chúng ta lại quan tâm đến mô hình sản sinh dữ liệu và nó có vai trò gì trong học máy và khoa học dữ liệu. Như chúng ta có thể đã nghe và biết, ngày nay dữ liệu rất nhiều và phong phú. Tuy nhiên, trong các ứng dụng đặc thù bên y học, công nghệ, và tài chính, việc thu thập dữ liệu mới nhiều khi rất tốn kém. Vì vậy, việc chúng ta có thể sản sinh ra dữ liệu mới thông qua những dữ liệu có sẵn không những giúp chúng ta hiểu nhiều hơn về dữ liệu mà còn giúp tiết kiệm được rất nhiều chi phí trong trong thực tế. Tuy nhiên, ngày nay dữ liệu chúng ta thu thập được thường có số chiều không gian cực kỳ lớn (có thể lên đến vài trăm ngàn hay vài triệu). Việc xây dựng mô hình sản sinh dữ liêụ trong không gian cao chiều là một bài toán rất khó vì các phương pháp cố điển bên học máy và khoa học dữ liệu, như kernel density estimation, bị hai vấn đề cốt lõi: (i) curse of dimensionality, tức là chúng ta cần một số lượng rất lớn dữ liệu để có thể hiểu được hiệu quả cơ chế sinh ra dữ liệu; (ii) không thể nắm giữ một cách hiệu quả các thuộc tính trong dữ liệu do số chiều quá lớn và có nhiều chiều không mang thông tin hữu ích về dữ liệu.

Trong bài blog này, dựa vào những ý tưởng trước đây chúng ta đã có được từ định lý tích phân Fourier về việc ước lượng hàm mật độ, chúng ta sẽ chỉ ra rằng có thể xây dựng được một mô hình hiệu quả để sản sinh ra dữ liệu từ định lý này và không bị hai vấn đề nêu trên của các phương pháp cổ điển. Chi tiết hơn cho phương pháp này có thể đọc tại [1]. Để cho thuận tiện cho việc thảo luận và trình bày, chúng ta sẽ phát biểu Toán học một cách chặt chẽ hơn cho bài toán của mình. Giả sử chúng ta có dữ liệu $X_{1}, \ldots, X_{n}$ trên $d$ chiều được sản sinh ra từ một phân phối xác suất $P$. Điều chúng ta quan tâm là có thể có tìm được một ước lượng của $P$ mà tại đó chúng ta có thể sản sinh ra các dữ liệu liệu tốt và có những đặc tính quan trọng giống với dữ liệu có sẵn. Để làm được điều này, chúng ta đầu tiên xài công thức phân rã nổi tiếng sau:

\[\begin{align*} P(x) = \prod_{j = 1}^{d} P(x_{j} \mid x_{1}, \ldots, x_{j - 1}), \end{align*}\]

với mỗi $x = (x_{1}, \ldots, x_{d})$. Như vậy, chúng ta chỉ cần ước lượng tốt các hàm phân phối có điều kiện (conditional distribution) \(P(x_j \mid x_1, \ldots, x_{j-1})\) với mọi \(j \in \{1, 2, \ldots, d\}\) là chúng ta sẽ có một ước lượng tốt đối với \(P(x)\).

Để ước lượng $P(x_{j} \mid x_{1}, \ldots, x_{j - 1})$, chúng ta sẽ sử dụng định lý tích phân Fourier. Thực vậy, chúng ta sẽ có ước lượng sau đây:

\[\begin{align} \widehat{F}_{R}(x_j\mid x_{1},\ldots,x_{j-1})=\frac{1}{2}+\frac{1}{\pi}\frac{\sum_{i=1}^n \text{Si}(R(x_j-X_{ij}))\,\prod_{l=1}^{j-1} K_{R}(x_l-X_{il})} {\sum_{i=1}^n \prod_{l=1}^{j-1} K_{R}(x_l-X_{il})}, \label{eq:cond_est} \end{align}\]

tại đây $K_{R}(z) =\sin(Rz)/z$ and $\text{Si}(z)=\int_0^z\sin (x)/x\,dx$ với mọi $z \in \mathbb{R}$. Chúng ta có thể chứng minh rằng $\widehat{F}(x_j\mid x_{1},\ldots,x_{j-1})$ là một ước lượng hiệu quả của phân phối có điều kiện $P(x_j \mid x_1, \ldots, x_{j - 1})$ ngay khi $R$ được chọn đủ tốt. Điều này có nghĩa là chúng ta có ngay một ước lượng tốt của $P(x)$ như sau:

\[\begin{align} \widehat{F}_{R}(x) = \prod_{j = 1}^{d} \widehat{F}_{R}(x_j\mid x_{1},\ldots,x_{j-1}). (1) \end{align}\]

Câu hỏi đặt ra bây giờ là làm sao chúng ta có thể sản sinh ra dữ liệu mới \(y = (y_{1}, \ldots, y_{d})\) từ \(\widehat{F}_{R}\). Thực vậy, để làm được vậy, chúng ta sử dụng phương pháp lấy mẫu tuần tự (sequential sampling) từ các ước lượng \(\widehat{F}(y_{j}\mid y_{1},\ldots,y_{j-1})\) với mọi \(j \in \{1, 2, \ldots, d\}\). Cụ thể hơn, đầu tiên chúng ta lấy mẫu \(y_{1}\) từ \(\widehat{F}_{R}(y_{1})\) bằng cách giải bài toán ngược \(\arg\inf_{y' \in \mathbb{R}} \,\, \widehat{F}_R(y')=u\) mà tại đây $u$ là một biến ngẫu nhiên (random variable) từ phân phối đồng đều (uniform distribution) trên đoạn $(0,1)$. Phương pháp lấy mẫu này được biết đến như inverse sampling approach (Các bạn có thể xem thêm tại đây). Bằng việc có \(y_{1}\), chúng ta sẽ lấy mẫu \(y_{2}\) từ \(\widehat{F}_{R}(y_2\mid y_{1})\) cũng bằng phương pháp inverse sampling. Chúng ta cứ tiếp tục quá trình này cho đến khi thu được \(y_{1}, y_{2}, \ldots, y_{d}\), có nghĩa là chúng ta đã có được một dữ liệu mới \(y = (y_{1}, \ldots, y_{d})\) từ ước lượng $\widehat{F}_{R}$ tại phương trình (1).

Một điều tuyệt vời của phương pháp trên là các ước lượng ở phương trình (1) là một dãy martigale (martingale sequence) và phương sai (variance) của nó có lẽ chỉ tăng một cách tuyến tính với số lượng chiều không gian. Điều này có nghĩa là phương pháp này sẽ hiệu quả cho dù số chiều không gian rất lớn. Để thấy được sự hiệu quả của mô hình sản sinh dữ liệu mà chúng ta vừa phát triển, chúng ta sẽ xem xét ví dụ sau. Giả sủ chúng ta có $n = 1000$ dữ liệu trong không gian $d = 100$ chiều. Lưu ý rằng, chúng ta có thể cho số chiều không gian lớn hơn nhiều như $d = 1000$ hay thậm chí $d = 10000$ và kết quả vẫn tương tự. Việc cho số chiều $d = 100$ để cho thuận tiện về mặt minh họa kết quả. Ở mỗi dữ liệu $x = (x_{1}, \ldots, x_{d})$, các đặc tính của nó được sản sinh từ một quy trình Markov. Cụ thể hơn, $x_{1}$ được sản sinh từ hàm phân phối chuẩn và

\[\begin{align*} x_{j + 1} = \rho x_{j} + \sqrt{1 - \rho^2} z_{j}, \end{align*}\]

với mọi $j \geq 2$ mà tại đây $z_{j}$ là một dãy các biến ngẫu nhiên với phân phối chuẩn. Chúng ta chọn $\rho = 0.9$, tức là chúng ta có một sự phụ thuộc rất lớn giữa các đặc tính trong dữ liệu. Kết quả dữ liệu mới được sản sinh từ phương pháp của chúng ta được trình bày tại Hình 1. Như chúng ta có thể thấy từ Hình 1, dữ liệu mới nắm giữ được các đặc tính quan trọng từ các dữ liệu cho sẵn.

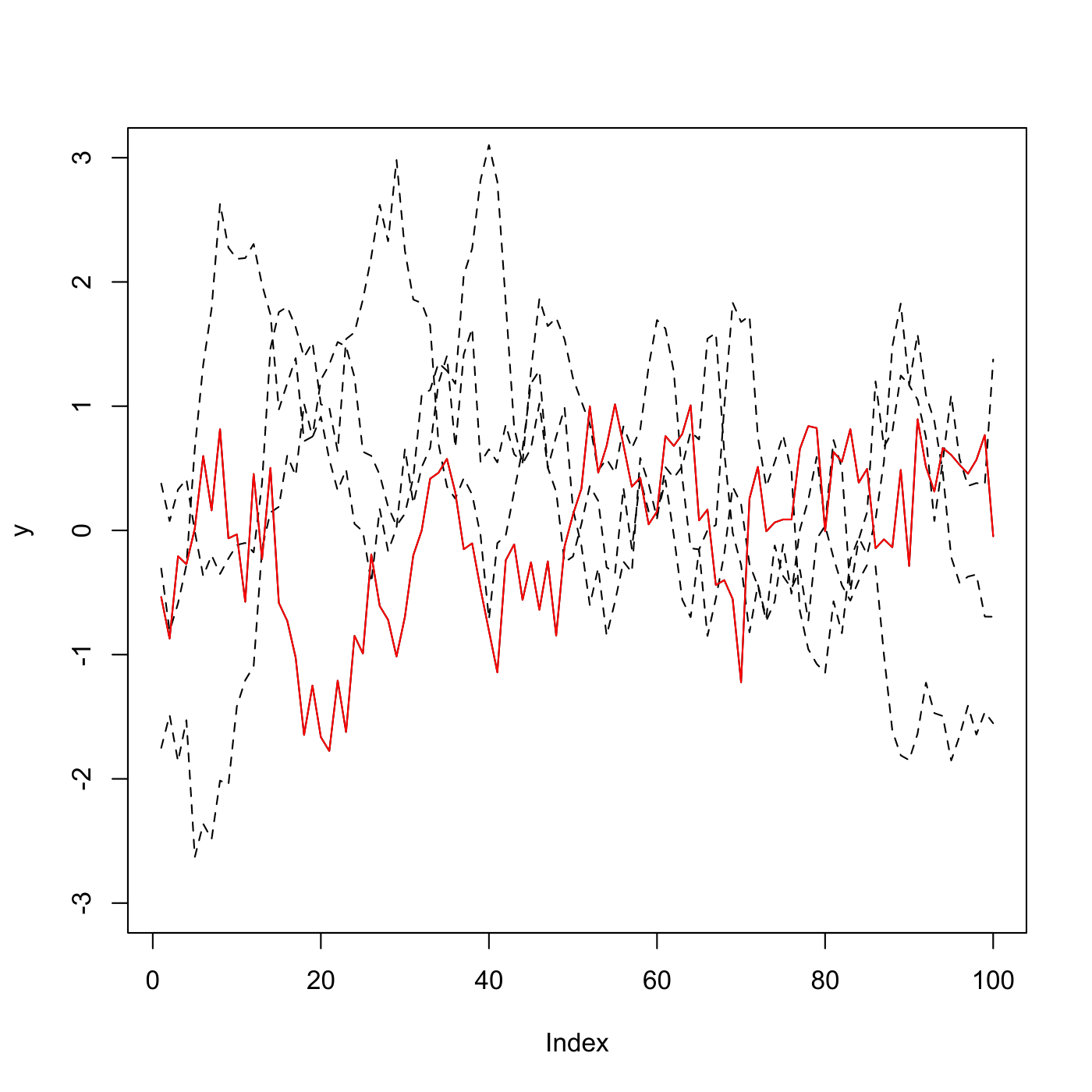
Kết luận:

Như vậy, chúng ta đã phát triển được một phương pháp hiệu quả để sản sinh dữ liệu mới từ các phân phối trên không gian cao chiều. Điều quan trọng là phương pháp của chúng ta cho ta những ước lượng tường minh mà tại đó chúng ta có thể định lượng được sự không chắc chắn (uncertainty quantification) từ các dữ liệu mới. Điều này phần nào giải quyết được vấn đề nan giải mà các mô hình blackbox như GAN và VAE hiện tại đều không làm được hiệu quả.

Tài liệu tham khảo

[1] N. Ho and S.G. Walker. Statistical analysis using the Fourier integral theorem. Arxiv preprint Arxiv: 2106.06608, 2021.

Top