Ước Lượng Hàm Mật Độ (Density function estimation)

Trong phần đầu tiên của blog này, chúng ta sẽ thảo luận về ứng dụng của định lý tích phân Fourier (Fourier integral theorem) cho vấn đề ước lượng hàm mật độ trong khoa học dữ liệu và học máy. Một câu hỏi tự nhiên mà mọi người có thể đặt ra là vì sao chúng ta lại quan tâm đến hàm mật độ và nó có ứng dụng gì trong khoa học dữ liệu.

Mình sẽ nêu một ví dụ đơn giản của hàm mật độ thông qua các dữ liệu về ảnh. Giả sử chúng ta có tập hợp các ảnh về chữ số và trong mỗi ảnh sẽ là tập hợp các điểm ảnh (pixel). Như vậy, chúng ta có thể coi mỗi ảnh là vector trên không gian nhiều chiều và mỗi chiều tương ứng với 1 điểm ảnh. Chẳng hạn với các ảnh từ bộ dữ liệu nổi tiếng MNIST, mỗi ảnh sẽ là một vector trên không gian 784 chiều, tương ứng với độ dài 28*28, và mỗi chiều tương ứng với 1 pixel. Giờ đây, với một tập hợp các ảnh cho trước, chúng ta có thể coi tập hợp này như tập hợp các vectors trên không gian nhiều chiều.

Trên thực tế, mặc dù các ảnh đều về một chữ số nhất định, chẳng hạn như về số 0, thì các ảnh đều có sự khác biệt một ít về hình dạng và cấu trúc. Sự khác biệt này có thể coi đến từ sự ngẫu nhiên của các điểm ảnh trong một bức ảnh nhất định, tức là, có một phân phối xác suất nào đó (probability distribution) sản sinh ra các điểm ảnh này. Đáng tiếc, phân phối xác suất này mình thường không biết và chỉ có thể ước lượng thông qua các bức ảnh hay chung lại là dữ liệu. Việc ước lượng hàm mật độ là một cách để hiểu được đặc tính của các phân phối xác suất này và từ đó giúp chúng ta có thể hiểu được cơ chế sản sinh ra dữ liệu.

Giờ đây, chúng ta sẽ phát biểu Toán học một cách chặt chẽ hơn cho bài toán ước lượng hàm mật độ. Giả sử chúng ta có dữ liệu $X_{1}, \ldots, X_{n}$ trên $d$ chiều được sản sinh ra từ một phân phối xác suất $P$ và phân phối xác xuất này có hàm mật độ là $p$. Mục tiêu của chúng ta là ước lượng hàm mật độ $p$ thông qua dữ liệu $X_{1}, \ldots, X_{n}$.

Kernel density estimation (KDE):

Một phương pháp rất phổ biến để ước lượng hàm mật độ là kernel density estimation. Ý tưởng của phương pháp là chúng ta làm trơn (smooth) mỗi điểm dữ liệu bằng một hàm hạt nhân và từ đó combine các hàm hạt nhân này lại để ước lượng hàm mật độ. Cụ thể hơn, chúng ta có ước lượng hàm mật độ như sau:

\[\begin{align} \widehat{p}_{H}(x) = \frac{1}{n} \sum_{i = 1}^{n} K_{H} \bigr(x - X_{i} \bigr), (1) \label{eq:kde} \end{align}\]

trong đó $K_{H}(x) = |H|^{-1/2} K(H^{-1/2}x)$ với mọi giá trị của $x \in \mathbb{R}^{d}$, $K$ là hàm hạt nhân (kernel function) không âm, và $H$ là ma trận băng thông (bandwidth matrix) có tính chất đối xứng (symmetric) và positive definite. Trong các ứng dụng thực tế, chúng ta thường chọn hàm hạt nhân \(K\) là phân phối Gaussian (Gaussian distribution) trong đó $H$ được chọn là ma trận hiệp phương sai (covariance matrix).

Tuy nhiên, có 2 vấn đề nền tảng đối với ước lượng (1). Thứ nhất, ma trận $H$ mang vai trò rất quan trọng trong việc nắm giữ tính chất phụ thuộc giữa các chiều không gian hay còn gọi là đặc tính của dữ liệu. Chẳng hạn, việc tương tác giữa các điểm ảnh trong một bức ảnh cần được thể hiện một cách khá chính xác thông qua việc chọn ma trận $H$. Điều này dẫn đến việc chúng ta phải chọn ma trận $H$ rất cẩn thận trong thực tế để ước lượng (1) thực sự hoạt động hiệu quả. Thứ hai, số lượng dữ liệu để ước lượng (1) có thể xấp xỉ tốt hàm mục tiêu $p$ sẽ tăng theo số chiều. Chẳng hạn, nếu số lượng dữ liệu bạn cần lúc 1 chiều là 1000 dữ liệu thì lúc lên 100 chiều, con số này có thể tăng lên 100000 dữ liệu.

Định lý tích phân Fourier (Fourier integral theorem):

Giờ đây chúng ta sẽ chứng minh rằng có thể giải quyết vấn đề chọn ma trận $H$ thông qua một định lý rất nổi tiếng: Định lý tích phân Fourier. Cụ thể hơn, với một hàm $f: \mathbb{R}^{d} \to \mathbb{R}$ thỏa mãn một số điều kiện nhất định, chúng ta có:

\[\begin{align} f(y) = \frac{1}{\pi^{d}}\lim_{R\to\infty} \int \prod_{j=1}^d \frac{\sin (R(y_j-x_j))}{y_j-x_j}\,f(x)\,d x. \label{eq:Fourier_theorem} (2) \end{align}\]

Tại đây, $x = (x_{1}, \ldots, x_{d})$ và $y = (y_{1}, \ldots, y_{d})$. Kết quả (2) đến từ hai kết quả rất đẹp trong toán học: phép biến đổi Fourier (Fourier transform) và phép biến đổi nghịch đảo Fourier (Fourier inverse). Kết quả (2) về cơ bản nói rằng cho dù các chiều không gian trong dữ liệu có phụ thuộc lẫn nhau nhiều như thế nào thì việc chỉ lấy tích của các hàm sin vẫn hiệu quả trong việc hiểu được các sự tương tác này. Dựa vào kết quả này, chúng ta có một ước lượng mới cho hàm mật độ như sau:

\[\begin{align} \overline{p}_{R}(x) = \frac{1}{n \pi^{d}} \sum_{i = 1}^{n} \prod_{j=1}^d \frac{\sin (R(x_j-X_{ij}))}{x_j-X_{ij}}. \label{eq:Fourier_esitmator} (3) \end{align}\]

Tại đây, $x = (x_{1}, \ldots, x_{d})$, $X_{i} = (X_{i1}, \ldots, X_{id})$ với mọi $i \in {1,2,\ldots, n}$. So với ước lượng (1) mà việc chọn ma trận $H$ thường rất khó trong thực tế, chúng ta chỉ cần chọn một tham số duy nhất $R$ trong ước lượng (3) để xấp xỉ hàm mật độ $p$ và vẫn có thể nắm giữ được sự phụ thuộc giữa các chiều dữ liệu một cách hiệu quả.

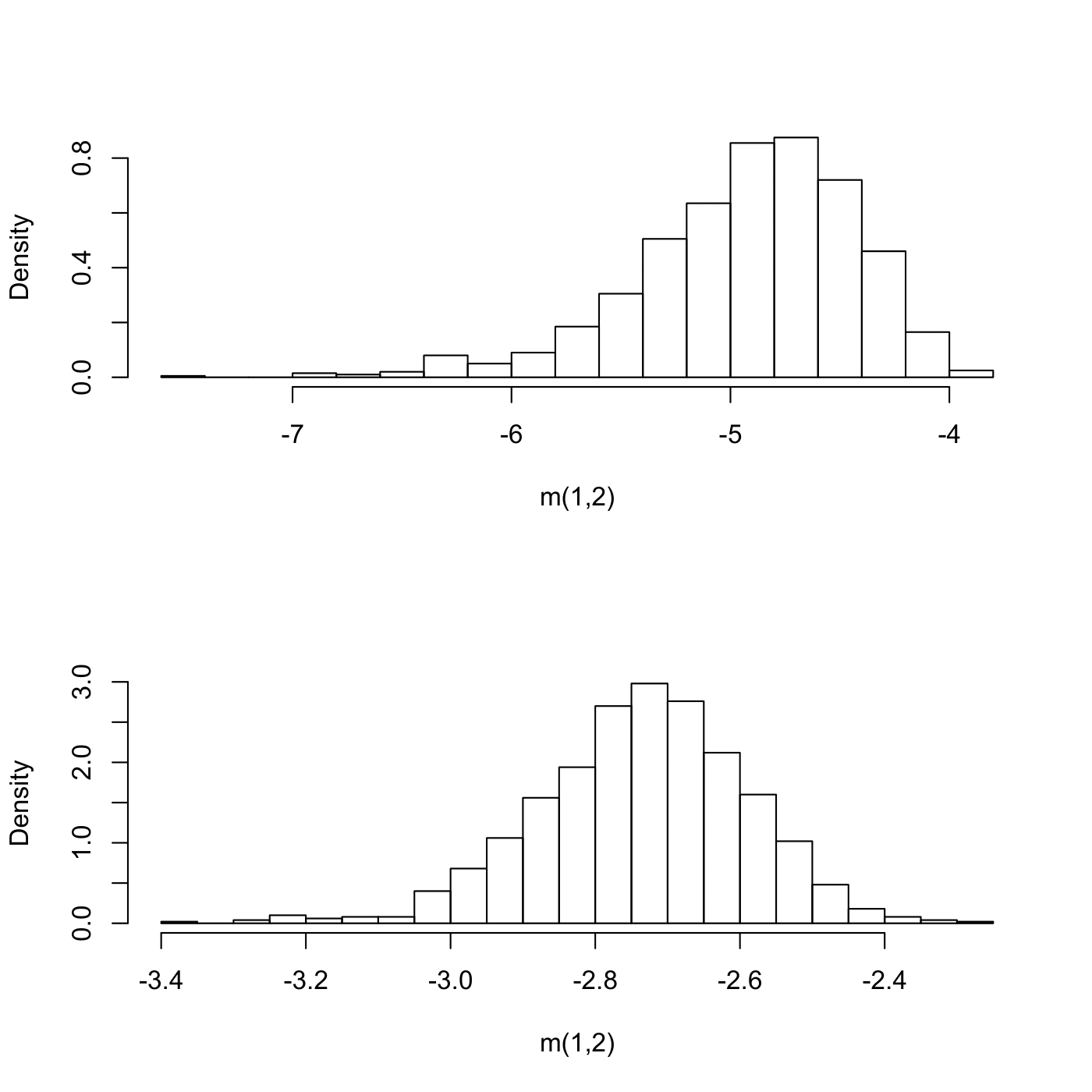
Để thấy rõ hơn sự hiệu quả của ước lượng (3), chúng ta sẽ so sánh nó với ước lượng (1) khi hàm hạt nhân $K$ được chọn là phân phối Gauss. Chúng ta sẽ sử dụng thí nghiệm về hồi quy không tham số (nonparametric regression) trong Ví dụ 1 của bài báo [1]. Kết quả của thí nghiệm ở Hình 1. Trong ví dụ này, chúng ta muốn hàm mật độ mà chúng ta ước lượng sẽ tập trung xung quanh -5. Từ Hình 1, chúng ta có thể thấy rằng ước lượng hàm mật độ từ Fourier cho kết quả chính xác hơn rất nhiều ước lượng (1). Lý do ước lượng (1) không cho kết quả tốt vì nó không thể nắm giữ được sự phụ thuộc giữa các đặc tính của dữ liệu một cách hiệu quả trừ khi chúng ta có thể chọn rất tốt ma trận $H$. Trong khi đó, ước lượng từ Fourier có thể nắm được sự phụ thuộc giữa các đặc tính một cách hiệu quả và chúng ta chỉ cần chọn tham số $R$, vốn dĩ dễ dàng hơn rất nhiều so với việc chọn ma trận $H$.

Kết luận:

Như chúng ta có thể thấy, định lý tích phân Fourier cho chúng ta một công cụ rất mạnh để ước lượng hàm mật độ của dữ liệu cho dù các thuộc tính trong dữ liệu có sự phụ thuộc rất mạnh. Đây là một tin tức rất tốt vì nó cho chúng ta một hy vọng về việc xây dựng ước lượng hiệu quả cho phân phối xác suất của dữ liệu trên không gian cao chiều, một vấn đề mà hiện tại chúng ta phải dùng đến những mô hình black-box như GANs hoặc VAE để có thể phần nào giải quyết được.

Tài liệu tham khảo

[1] N. Ho and S.G. Walker. Multivariate smoothing via the Fourier integral theorem and Fourierkernel. Arxiv preprint Arxiv:2012.14482, 2021.

Top